Insbesondere beim Klimaunfug vertraut man „der Wissenschaft“, genauer: irgendwelchen Rechenmodellen, die irgendeinen Horror ausrechnen und im Gegenzug ein Paradies voraussagen, sofern man bereit ist, 90% seines Einkommens in irgendetwas zu investieren, das sich mit Sicherheit als persönlicher Horror erweist und obendrein nicht funktioniert. Komischerweise wird den Berechnungen, die das Nichtfunktionieren nachweisen und im Gegensatz zu den anderen Modellen meist nur Dreisatz und Prozentrechnung benötigen, wieder nicht vertraut.
Dabei ist angesagt, den Modellen gegenüber eher misstrauisch zu sein. In dieser „Wissenschaft“ stecken nämlich mindestens 3 Ursachen dafür, dass bei den ganzen Rechnereien ziemlicher Unfug heraus kommt:
- Ein Modell, in dem das gewünschte Ergebnis bereits vorgefertigt eingebaut ist,
- eine dilettantische Umsetzung, die zu nicht mehr durchschaubaren Code und damit automatisch zu mehr Fehlern als korrekten Daten führt und
- durch die Rechenleistung des Computers selbst, der zu völlig unsinnigen Ergebnissen führt, wenn der Programmierer keine Ahnung von numerischer Mathematik hat.
Zwar vermutlich vergebene Liebesmüh, aber ich versuche trotzdem einmal, die Ursachen ein wenig zu beleuchten. Dabei geht es nicht konkret um (oder gegen) die Modelle, sondern um die Grundlagen, auf denen diese Modelle basieren. Wenn nicht mehr kritiklos alles geglaubt wird, sondern ein Bewusstsein entsteht, dass man auch Fragen stellen kann, ist schon einmal ein Anfang gemacht.
Wir schauen uns heute einmal 3. an. Computer berechnen alles mit den 4 Grundrechenarten Addition (+), Subtraktion (-), Multiplikation (*) und Division (/) aus. Das gilt auch für komplexe mathematische Funktionen oder das Lösen irgendwelcher Gleichungssysteme oder Differentialgleichungen oder Integrale oder sonst was, also alles Zeug, von dem viele keine Ahnung haben, von dem sie aber so überzeugt sind, dass sie sich auf die Straße kleben.
Die meisten Berechnungen basieren darauf, dass ein Wert berechnet wird und dieser wieder als Ausgangspunkt für den nächsten Rechenschritt dient. Beispielsweise berechnet die folgende Formel aus dem Wert n, beispielsweise 15, den Wert 2n, also 30. Weitere Formeln solcher Art dienen dann dazu, die Werte 1, 2, 3, … 14, 16, .. 29 zu berechnen und das das Endergebnis liegt bei beispielsweise n=1.500 vor.
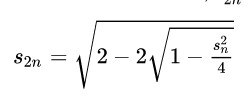
Wenn sich nun bei n=15 ein Fehler eingeschlichen hat, wird dieser dazu führen, dass auch n=30 fehlerhaft ist und letztlich auch das Endergebnis unbrauchbar wird. Also gilt es, das zu vermeiden. Wobei der Computer die Fehler auch von alleine machen kann und keine Hilfe dazu benötigt, wie wir sehen werden.
Solche Formeln sind zwar auch mit einiger Mühe direkt mit einem Taschenrechner auswertbar, aber im Computer wird letztlich alles durch Operationen wie
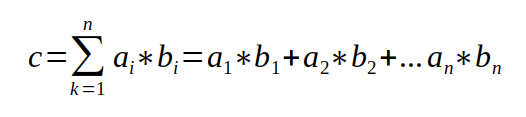
ausgerechnet, wobei die Zahlen rechts vom Gleichheitszeichen dem Computer bekannt sind und der eben die Zahl links neu ausrechnet. Auch die Wurzelformel wird intern durch solche Operationen abgebildet, wobei einfachere Sachen durch Hardware oder Standardsoftware abgebildet werden, komplexere aber vom Programmierer kodiert werden müssen.
In der Formel steht zwar überall + , aber wenn ein Produkt positiv, das nächste negativ ist, läuft das auf eine Subtraktion hinaus, wie hoffentlich jeder versteht.
Was kann dabei schief gehen? Nun, zunächst sind die Zahlen nicht ganz genau, weil der Computer beispielsweise Brüche nur als Dezimalzahlen speichern kann. Dazu wird auf den nächsten darstellbaren Wert gerundet.
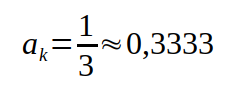
Ist x der exakte Wert, speichert der Computer den Wert y
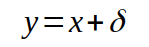
wobei das delta der Fehler bei der Speicherung ist (hier 0,00003333…), der positiv oder negativ sein kann (wir wissen es nicht, d.h. bei 1/3 schon, aber im Allgemeinen eben nicht). Der Wert 0,3333 ist also nur bis auf den maximalen Rundungsfehler 0,3333 +- 0,00005 genau. Auch für Messwerte, die vom Programm verarbeitet werden, gilt das, denn die Messgenauigkeit, beispielsweise für die Temperatur, ist ebenfalls begrenzt.
Die Fehler gehen natürlich auch in die Rechnungen ein. Bei einer echten Addition wird daraus
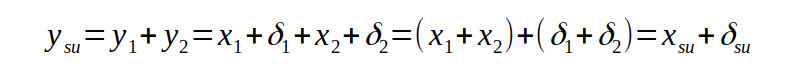
Wenn die deltas gleich groß sind, ist der maximale Ergebnisfehler doppelt so groß wie die Eingangsfehler. Würden wir die Näherung für den Bruch 1/3 zu sich selbst addieren, wäre das Ergebnis
0,3333 + 0,3333 = 0,6666
Bei exaktem Rechnen käme allerdings etwas anderes heraus:
1/3 + 1/3 = 2/2 = 0,6667
Weil die Rundung nun nach oben laufen müsste. Das Ergebnis auf dem Computer ist also nicht korrekt, wobei normalerweise mit 15 Stellen hinter dem Komma gerechnet wird, d.h. die Abweichungen tun nicht wirklich weh. Da in längeren Rechnungen aber Fehler positiv oder negativ sein können, mittelt sich vieles auf Dauer auch wieder heraus, so lange die deltas klein und untereinander vergeichbar sind, d.h. bei der Addition kommt es normalerweise nicht zu (größeren) Fehlern.
Bei der Plutimikation Multiplikation sieht das so aus:
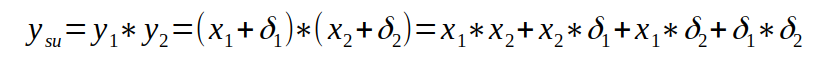
Den letzten Term kann man vergessen, da das Produkt aus zwei kleinen Größen keine Rolle spielt, da es noch kleiner ist. Formen wir den Rest etwas um, ist das Verhältnis zwischen berechnetem und exaktem Wert
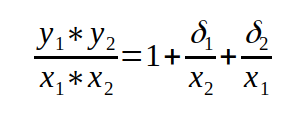
So lange die deltas klein im Verhältnis zu den Zahlen selbst und untereinander vergleichbar sind, weicht das Verhältnis nicht merklich vom Wert 1 ab und wir kommen zu dem gleichen Schluss wie bei der Addition: der Gesamtfehler bleibt klein und macht keine Probleme.
Genauso bleibt es bei der Division. Die lässt sich auf die Multiplikation zurückführen, indem man den Bruch mit dem Faktor 1 in einer speziellen Form erweitert:
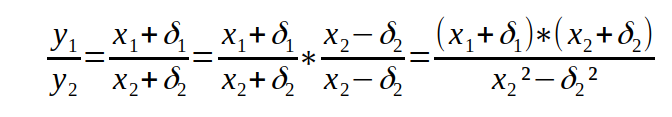
Ob + oder – bei den deltas spielt keine Rolle, da wir den Fehler ohnehin nicht kennen, also können wir wahlweise + oder – setzen. Im Nenner steht nichts Aufregendes, im Zähler eine normale Multiplikation.
Bei der letzten Operation, der Subtraktion, sieht es vordergründig auch unkritisch aus. Wenn wir uns um das Vorzeichen der deltas wieder nicht kümmern, gelangen wir zu
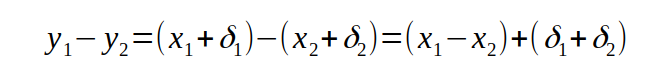
und das Verhältnis der berechneten zu den korrekten Werten wird zu
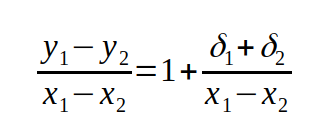
Wenn die deltas klein sind und sich die Werte stark unterscheiden, also doe Differenz auch groß bleibt, ist das Verhältnis wieder in der Nähe von 1 und alles ist im grünen Bereich. Ein Problem entsteht allerdings, wenn die Differenz der Werte sehr klein wird. Machen wir uns das an einem Zahlenbeispiel klar.
Wie wir oben gesehen haben, müssen wir bei den deltas davon ausgehen, dass sie mindestens dem Rundungsfehler entsprechen. Nehmen wir einmal an, dass noch nichts Schlimmes passiert ist, wäre das für unser 1/3-Beispiel im schlimmsten Fall (beide deltas haben das gleiche Vorzeichen und sind gleich groß)
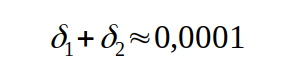
Nehmen wir weiter an, bei einer exakten Rechnung betrage die Differenz
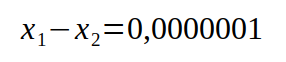
Dann folgt daraus
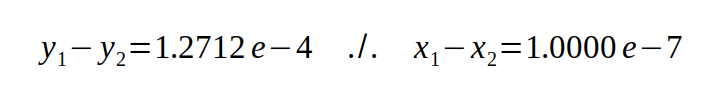
Um das zu verstehen, muss man berücksichtigen, dass ein Computer immer mit der maximal zur Verfügung stehenden Stellenanzahl rechnet und dazu alle vorderen Nullen ausblendet. Die Potenz gibt an, wie viele Nullen ausgeblendet werden. In unserem Beispiel kodiert der Rechner folglich
1/3 = 0,3333 = 3,333 * 10⁻¹
Bekommt er bei einer Subtraktion führend Nullen heraus, macht er das natürlich auch, d.h.
y = 0,001 * 10 ⁻¹ = 1,000 * 10⁻⁴
und da er nicht mit Zehnerpotenzen rechnet, sondern mit 2er-Potenzen, können dann nach Umrechnung in das Dezimalsystem tatsächlich so merkwürdig Zahlen herauskommen wie oben angegeben. Das fatale an der Sache: man sieht es der Zahl gar nicht an, dass von den 5 Stellen vielleicht nur die erste korrekt ist, sich die anderen 4 Stellen der Computer aufgrund von Rechenfehlern mehr oder weniger selbst ausgedacht hat. Es kann sogar noch Schlimmer kommen:
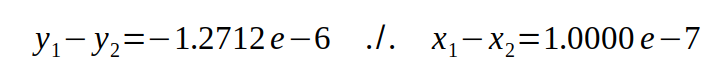
Hier ist der berechnete Wert nicht nur völlig falsch, er hat obendrein auch noch das falsche Vorzeichen.
Wird jetzt mit solchen Werten, bei denen das delta in der gleichen Größenordnung wie die Zahl selbst liegt (oder darüber) und das Vorzeichen ebenfalls nicht mehr stimmt, weiter gerechnet, kommt natürlich auch bei der Addition, der Multiplikation oder der Division nur noch Schrott heraus. In einer Beispielrechnung für den Wert von PI sieht das beispielsweise so aus:
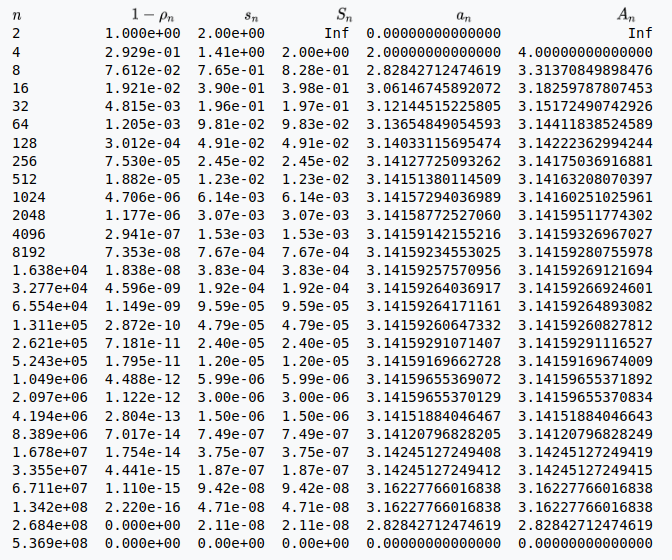
Nachdem alles anfänglich in die richtige Richtung läuft, ändert sich das schnell und zum Schluss kommt der Wert NULL für PI heraus. Alle Formeln dabei sind korrekt, aber der Rechner macht eben Fehler, wenn er bei der Subtraktion gleich große Werte voneinander subtrahiert.
Die Berechnung von PI ist natürlich aufwändig, aber selbst bei einfachen Sachen kann das schief gehen. Es lassen sich Beispiele mit 2 Gleichungen und 2 Unbekannten konstruieren (dabei werden aus 6 Ausgangswerte die zwei Unbekannten berechnet; das ist hoffentlich noch banaler Schulstoff), bei denen im Ergebnis nicht eine einzige Ziffer korrekt ist, obwohl der Computer mit 16 Stellen Genauigkeit rechnet.
Bei der Programmierung muss man auf so etwas achten. Man muss die Formeln so umbauen, das Subtraktionen vermieden werden, oder mit anderen Methoden arbeiten, die Korrekturen oder das Erkennen von Fehlern erlauben, so dass man die Rechnung anhalten kann, wenn alles aus dem Ruder läuft. Beispielsweise kann man die verwendeten Formeln im letzten Beispiel so umbauen, dass das richtige Ergebnis heraus kommt:
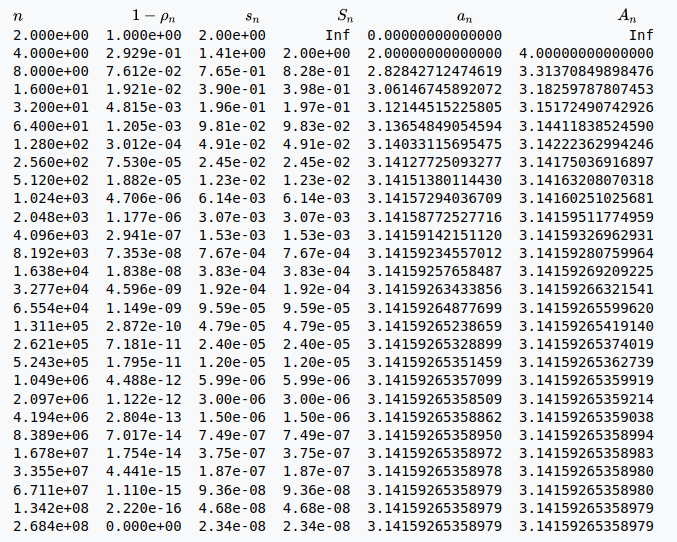
Bei vielen verschiedenen Formeln und sehr komplexen Programmen ist das natürlich nicht so einfach. Da verliert der Programmierer schon mal die Übersicht – falls er überhaupt von dieser Problematik weiß. Sehr viele dürften bereits überfordert sein, wenn es um das Erkennen solcher Ausreißer geht, ganz zu schweigen von den mathematischen Tricks, mit denen man das abstellt. Hier ein Beispiel:
Wie der Autor darlegt, hat man, statt sich um die Modellerierung und die Mathematik zu kümmern, sich kurzerhand darauf beschränkt, irgendwann unsinnige Ergebnisse zu erkennen und von Hand zu korrigieren. Dabei können allerdings schon etliche Rechenschritte mit kaputten Werten durchgeführt worden sein, die zu völligem Unsinn an anderer Stelle führen, der aber gar nicht erkannt werden kann.
Wie kann man diese Kenntnisse praktisch nutzen? Wenn jemand ein Rechenmodell vorstellt (beispielsweise ein Klimamodell), kann man ihn ja mal fragen, mit welchen mathematischen Methoden er das angegangen ist. Meist kommt die Ausrede „das verstehst du nicht“, aber ein paar Formeln wird er sicher irgendwann rausrücken und auch über Iteration (oder Rekursion) ein Wort verlieren. Die Fangfrage lautet „und wie hast du die Iteration numerisch stabilisiert?„. Kommt jetzt ein ratloser Blick …