Manchmal findet man Leute (selbst in der Politik), die was Vernünftiges sagen:

Nun, irgendwie hat Kretschmer ein wenig Recht, denn bei ein wenig Nachdenken wird man dem Irrationalen in der Argumentation, dass
- man von einem preiswerten und zuverlässigen Lieferanten „abhängig“ war und sich aus der Abhängigkeit und den Risiken befreit hat, indem
- man zu einem überteuerten und unzuverlässigen Lieferanten wechselte,
wohl kaum entfliehen können. Und wer auf das Argument
- eine Reparatur mit Kosten von 100 Mio € von einem Wertgegenstand im Wert von 8.000 Mio € lohnt sich
nicht eingeht, bringt seinen Maseratti vermutlich auch auf den Schrottplatz, wenn der Aschenbecher voll ist. Gleichwohl sind Gazetten, Stunk und Blödsehen und Politschwafler natürlich sofort mit persönlichem Bashing unterwegs. „Nationales Interesse“ und eine „Zeit nach dem Krieg“, denn außer A.B. niemand erklärt hat, das geht ja gar nicht.
Aus mathematischer Sicht stellt sich die Frage, wie die Vollverblödung der politischen und journalistischen Klasse bei dieser Art der Diskussion mit einer Stimme noch beschrieben werden kann. Setzt man den Indexwert eines typischen Vertreters dieser Klasse auf „1“, so stellt sich der VQ (Verblödungskoeffizient) in der Bevölkerung so dar:
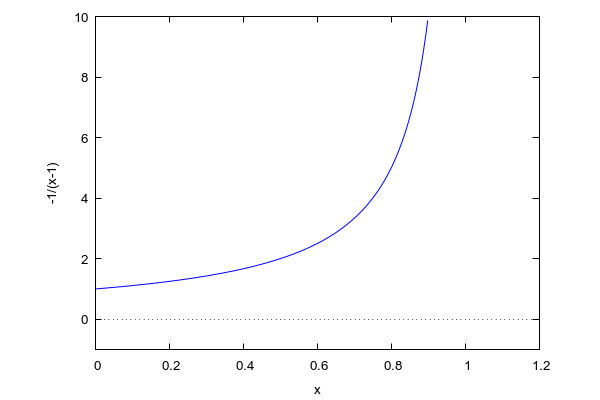
Wir können den VQ eines Politdarstellers folglich gar nicht ablesen. Selbst bei Veränderung des Maßstabs erleiden wir Schiffbruch
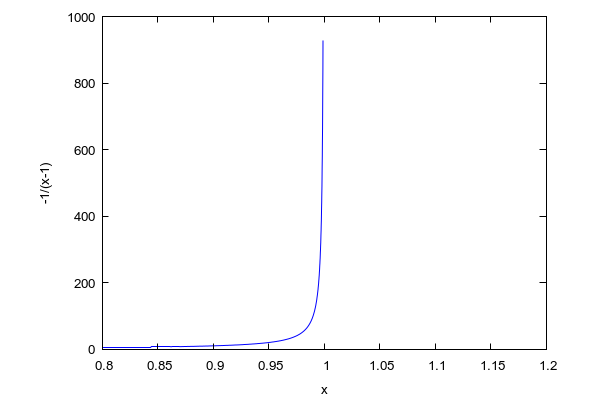
Für den VQ eines typischen Politikers oder Journalisten müssten daher inzwischen völlig neue Zahlen erfunden werden – mathematisch anscheinend ein Horror, denn die Menge R der reellen Zahlen reicht offenbar nicht aus und verhindert eine genaue mathematische Analyse des Problems.
Die die Mathematik wäre nicht die Mathematik, wenn sie nicht eine Lösung gefunden hätte. So simpel das auch klingt, es genügt, der Menge R einen Punkt hinzu zu fügen und das Problem ist gelöst:
Wie gesagt: genau einen Punkt, und zwar den unendlich fernen Punkt. Wie das das Problem beseitigt? Ganz einfach: auf der Menge R⁺ ḱann anstelle von VQ, der in R eine Unstetigkeitsstelle aufweist, die Funktion 1/VQ untersuchen. Und die sieht dann so aus:
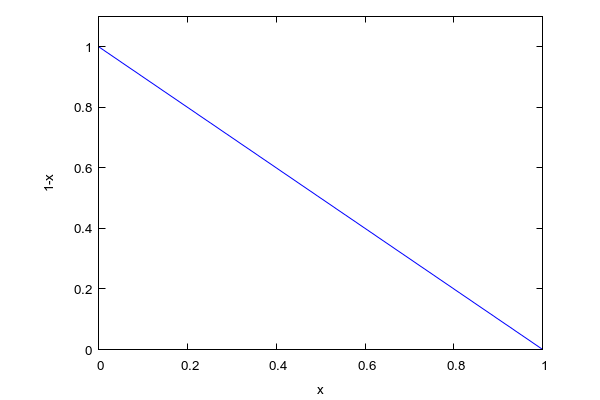
Aus einem unendlich steilen Verlauf der VQ-Kurve wird ein linearer und sehr einfach untersuchbarer Bereich der IQ=1/VQ – Kurve. Die Kurve ist vollstetig und lässt sogar Schlüsse auf die zukünftige Entwicklung des VQ der Politklasse in der Zukunft zu, die zu unendlich großen negativen Werten führt (was immer das auch bedeuten mag):
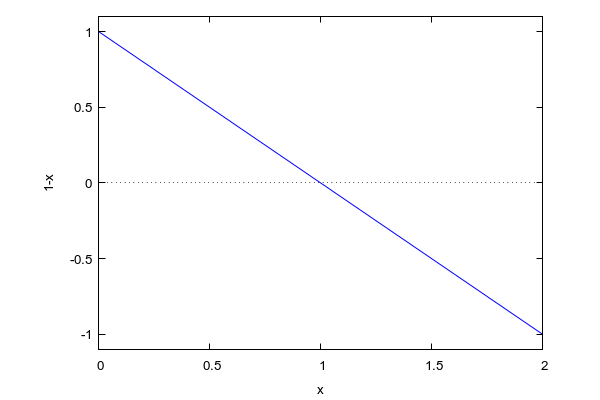
Allerdings ist die Indexierung „1“ für einen Vertreter der Politklasse problematisch. Besser wäre eine Darstellung, in der man die Leute einfach duchnummeriert und hier scheint diese Darstellung, die auch zeigt, wie schnell die Werte wachsen, angemessener:
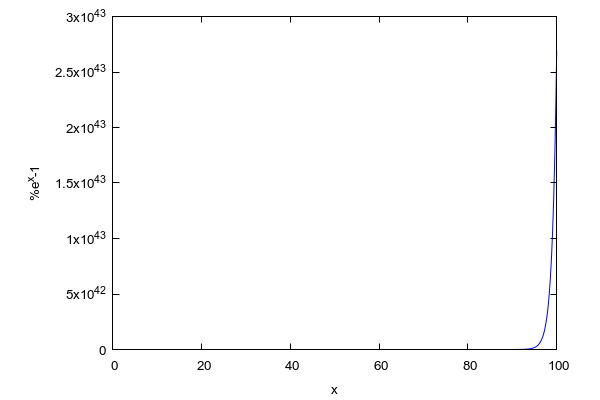
Und das geht nur bis zum Zählindex 100! Wollen wir das mathematisch erfassen, also den unendlich fernen unendlich verblödeten Politdarsteller exakt erfassen, hilft nur die doppelte Substitution, d.h. neben 1/VQ ist auch 1/x zu substituieren. Das liefert nun wirklich interessante Zusammenhänge:
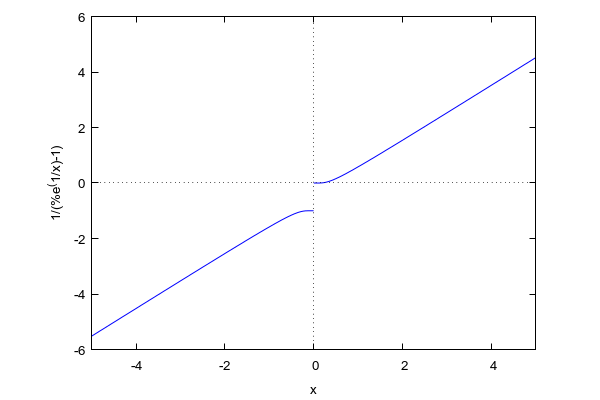
Wie man nämlich sieht, weist diese Funktion eine Unstetigkeitsstelle am Punkt
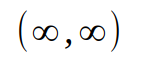
auf und das große, bislang noch ungelöste Rätsel ist, welchem Grünen-Politiker diese Unstetigkeitsstelle zukommt oder ob es sich gar um eine Mannigfaltigkeit handelt, also für die Belegung von x
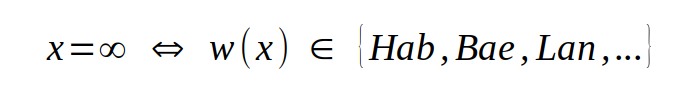
gilt. Will man noch genauer differenzieren, muss man in höhere Dimensionen wechseln. Trennt man Politiker und Journalisten, sieht das beispielsweise so aus
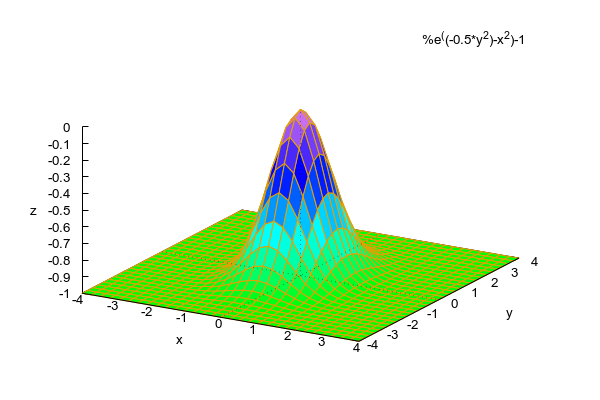
Wenn man noch feiner wird, wird es grafisch allerdings problematisch. Selbst nach 20 Jahren werden im Kino immer noch „nur“ Filme in 3D angeboten. Eine 12-dimensionale Darstellung der Eigenschaften auch nur der 11 wichtigsten Panneköppe scheitert daher an den Möglichkeiten der Technik, selbst hier.
Hinweis: das ist keine Erfindung von mir, sondern nennt sich Funktionentheorie.
Das hat übrigens interessante Auswirkungen auf die (projektive) Geometrie. Das Veblen-Young-Axiom sagt:
Wenn A, B, C, D vier Punkte sind, so dass die Gerade AB die Gerade CD trifft, so trifft die Gerade AC die Gerade BD.
Der geneigte Leser mag sich das anhand einer Skizze einmal klar machen und sich gleichzeitig überlegen, weshalb sich durch dieses Axiom Parallelen – Lieblingskind der Geometrie mit Zirkel und Lineal – erledigen. Es gibt keine Parallelen, was auch einige Interpretationen der Geschichte erledigt.
Für den, der bei der Überlegung dem geistigen Durchdrehen nahe kommt, empfehle ich:
Bei Politheinis übrigens völlig wirkungslos.